Rainbow Equation 3D Axis

c.=3d axis=(3f. rainbow sphere )+(3f. rainbow tetrahedron)

 The third axis (c.) of the Rainbow Equation is 3D. In this axis complements between linear and circular 3D models are shown. Using the rainbow as a guide the 3F Rainbow Sphere and Tetrahedron are shown to flow in similar patternization and mathematical flow. Applying the process of “third stacking”, also known as third frequency, produces sectors on the outside and inside of these seemingly opposing 3D models. The cutting across the models in even ratios allows for the polarities of the rainbow to flow externally and internally. As with the other 3D models, this cutting across or stacking produces smaller units that are hollow inside. All the sectors – sh.o., sh.i., i.s., i.s.i., are accounted for and align with the flow of the rainbow structure per color and sector.

The 3rd frequency Rainbow Sphere shell colorization follows the same patternization as its 2D counterpart, the Logos Circle Seven, representing the dimensional expansion from plane to third dimension. 


In the 3F Rainbow Sphere (3f.r.sph.) there are two complete neutral polarity rainbows upon its shell. Representing the two polarities of the core axis at the top and bottom of the 3f.r.sph. are white sectors, accounting for 4 white sectors inside and out. Since the inherent structure of the 3f.r.sph. is a “rounded off Rubik's cube” the left/right, front/back, top/bottom align with the same size and shape central square sectors on both 3D rainbow models. The 3f.r.sph. shell colorization follows the same patternization as its 2D counterpart, the Logos Circle Seven, representing the dimensional expansion from plane to third dimension.

The outer shell is rainbow sectors in the secondary polarity combination (r.s.,s.c.) and primary combination on the shell's inside (r.s.,p.c.). The in-between sectors and in-between-in sectors are in exactly the same color and order as the 3F Rainbow Cube. The most central 3d shape in the very center of the 3f.r.sph. is in the shape of a cube. Walls of nine sectors flow just like the 3f.r.cube from the sphere's central cube and dissipate where the 3f. r. cube has had its corners “rounded off” to form the 3f.r.sph. Blending tri. and quad. combinations outside to inside allows for 22 neutral polarity rainbows (264 sectors) plus 4 white sectors.

The rainbow equation for 3f. Rainbow Sphere is:
 sh.o.=(r.s.,s.c.)=(2n.=24)...+2w.s....+...i.s.=(quad.s.*18=108)...+...
sh.i.=(r.s.,p.c.)=(2.n.=24)...+2w.s....+...
i.s.i.=(tri.p.x18.=108)......=(22n.=264)+4w.s.

The 3F Rainbow Sphere, which is the rounded off Rubik's Cube, in-between sectors and in-between-in sectors are in exactly the same color and order as the 3F Rainbow Cube. 


The 3F Rainbow Tetrahedron (3f.r.tet.) is a blending of tetrahedrons and octahedrons. There are 11 small tetrahedrons: 4 white ones on the tips of the larger 3f.r.tet., 6 rainbow colored ones on the shell and one small tetrahedron in the 3f.r.tet.'s exact center. In the stacking together of the 3f.r.tet., four octahedrons nestle in-between the four tetrahedral tips and the central tetrahedron.
Each octahedron touches one of its 8 sides to the four sides of the central tetrahedron and one of its sides to the bottom of the small tetrahedra that show as the 3f.r.tet's white tips. The remaining 6 tetrahedra show one of their four sides as a sector on the outside shell. It is important to know that in the stacking together of tetrahedra and octahedrons the faces never touch. The shell of a octahedron is composed of 8 equilateral triangles and connect their surface faces to the tetrahedra's faces. The inside and outside white sectors for the 4 tetrahedral tips equal 32 (4*4 outside)+(4*4inside). There are 11 tetrahedra which each have 8 total sectors for a total of 88 sectors throughout (11*8)=88. This is added to the 16 inside/outside sectors of each 4 octahedrons to equal: (16*4)=64. Therefore there are 152 total sectors on the 3f.r.tet. Since 32 of these sectors are white sectors, there are 120 rainbow aspects or a total of 10 neutral polarity rainbows (152-32)=120.

The rainbow equation for 3f. Rainbow Tetrahedron is:
sh.o.=(2s.+2tri.s.=2n.)+12w.s....+ i.s.=(4.s.+4w.s.)...+
sh.i.=(2p.+2quad.p.=2n.)+12w.s....+i.s.i.=(4p.+4w.s.)
4s.+4p.=6n.
Rainbow aspects=(2n.+2n.+6n.)=10n. + 32 white sectors

The colorization of the 3F Rainbow Tetrahedron is described here:
The 4 tetrahedra tips are white inside/outside representing the axes of the 3f.r.tet. The outer shell is painted with 2 secondary polarity rainbows that flow around the three walls facing away from the 3f.r.cube. The fourth wall of the tetrahedron that faces the 3f.r.cube is tri-colors; orange-green-indigo, which flow into the triangular walls of the 3f.r.tet. of the rainbow colors above them. The following describes the colorization of the inside sectors. Looking at any of the 4 white tips, positioning in a way to view downward, there is white triangle plane that touches one of the 4 octahedrons below it. This bottom white triangle faces a triangular green top sector of the octahedron.

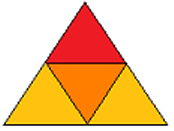Continuing to move downward from any of the four tips the triangular sector at the next layer (stacking), positioned horizontally to the green octahedron's sector is orange in color. This layer is a second frequency triangle, meaning one triangle surrounded by 3 other triangles. The orange is the central triangle and is surrounded by 1red-1yellow-1yellow triangle.  This 2F triangle is facing downward as one views from the top axis of any of the four tips. The next internal layer or stacking is the central tetrahedron. The outside of this tetrahedron is entirely indigo in the secondary color combination. On the inside is blue complementing the outer secondary color with a primary polarity color. All of the in-between-in colors are always in the primary polarity color complement.

 
Continue...