Rainbow Equation Table of Nicomachus
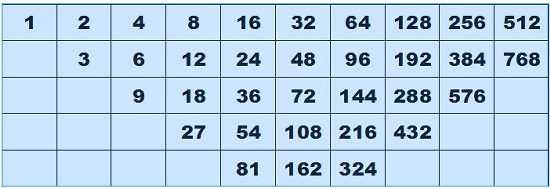
It was Greek mathematician Nicomachus of Gerasa, who lived in the first century, that brought humanity the Music of the Spheres – a relationship between music and the ordering of the universe. He viewed numbers as having mystical properties and was driven to understand what he termed the “divine number” relationship to the “scientific number.” The understanding and application of the harmonic system of numbers has been used as a model for musical compositions, architecture and the fine arts. It is Nicomachus who is credited for blending the divine into the scientific through “The Table of Nicomachus.” The table is a blending of the arithmetic and harmonic means. Taking any square of four numbers next to each other we can see the arithmetic mean. Looking at the number set of 2,4,6,3 for instance we see two arithmetic progressions – 2,3,4 and 2,4,6. The harmonic mean is also contained in any four numbers laid out in a square formation. (see table 8.3) The harmonic progressions are for this same square are 2,3,6 and 3,4,6. Each square of four numbers contain four ratios – ½, ⅓, ⅔, ¾. Moving from right to left = ½, moving diagonally top to bottom/left to right = ⅓, moving top to bottom = ⅔, moving diagonally bottom to top/left to right = ¾.The numbers and their ratios at the beginning of the Table of Nicomachus serve as the basis of musical harmony. Moving from left to right on the top line are relationships to octaves with the numbers – 1,2,4,8,16,32,64. The relationship to the perfect fifth is in ratio 3:2 such as seen in the octave of 6:12 whose arithmetic mean is 9. 9 in relation to 6 is 3:2, the perfect fifth. The harmonic mean of 6 and 12 is 8. In relation to 6, this proportion is 8:6 or 4:3, which is the perfect fourth. Using the successive multiplication by 3:2, the musical fifth, and 4:3, the musical fourth, is the method used by the Pythagoreans for generating the musical scale and is still the basis for reading, composing and playing music in the modern era. It is the harmonic ratios of music that show sound is organized into a mathematical symphony working in a natural rhythm with the ratios of light and the energetic field that governs all that manifests. These patterns are found through all of nature and can be shown to exist in Sacred Geometry and the Rainbow Equation.
| The “Language of Light” is now made manifest through the matrix of space and the rainbow. |
In the Rainbow Equation there is balance and harmony with nature. Within its structure and mathematics there is a blending between the divine and scientific number. Nicomachus of Gerasa was the first documented nearly two millenniums ago to see science and nature were able to be expressed in ratios and patterns in the language of mathematics. The counting of the Rainbow Equation's sectors is the mathematics of light and Sacred Geometry. Throughout the entire Rainbow Equation there are many connections to the ratios ½, ⅓, ⅔, ¾ that flow in “The Table of Nicomachus.” These total sector numbers contain the patternization found in the arithmetic and harmonic mean. These numbers of The Table of Nicomachus are the same numbers observed when counting the number of sectors in dozens of aspects of the various components of the Rainbow Equation. In the table's listing of 35 ratio numbers between 1 and 768 there are only five numbers that have not yet been discovered to show a direct connection to numerical values of the Rainbow Equation, with many Table of Nicomachus' numbers showing several relationships. The Rainbow Equation is this sacred balance between harmony (spirit) and science (matter). Through the process of connecting the visible spectrum of light with the dimensional ratios of Sacred Geometry a harmonic equation of light comes into being. The Language of Light is now made manifest through the matrix of space and the rainbow.
1 ~ Logos=Word, John 1:1 (Bible KJV) “In the beginning was the Word, and the Word was with God, and the Word was God.” The point, or Infinite Sphere
2 ~ one 3f.r.cube + one 4f.c.cube.
3 ~ one 3f.r.sph. + one 3f.r.cube + one 3f.r.tet. = the up, down axis
4 ~ 2f.tri.(composed of 4 triangles), 3f.r.sph.,w.s.
6 ~ spatial directions of 3d.space
8 ~ the octave, one 3f.r.sph. + one 3f.r.cube + one 3f.r.tet. + one l.c.7 + one t.s.c. + one s.s.s. + one 4f.3d.r.tri. + one w.s.v.e.
9 ~ 3f.square (composed of 9 squares), primary rainbow polarities, secondary rainbow polarities
12 ~ n.f.c.,r.sectors.,t.s.c., f.c.,r.sectors.,t.s.c., n.f.c.,r.lines t.s.c., f.c.,r.lines t.s.c., neutral rainbow polarities, 1f.hollow cube sectors
16 ~ 4f.square (composed of 16 squares)
18 ~ n.f.c.,r.s.,s.s.s., f.c.,r.s.,s.s.s.
24 ~ n.f.c.,r.s.,.l.c.7, f.c.,r.s.,l.c.7, n.f.c.,r.a.,s.s.s., f.c.,r.a.,s.s.s. n.f.c.,r.a.,t.s.c., f.c.r.a.,t.s.c., r.sectors 3f.r.tet., sh.o. r.sectors. 3f.r.tet.,sh.i., r.sectors 3f.r.sph.,sh.o. r.sectors 3f.r.sph.,sh.i. half cubes of the 4f.3d.r.tri.
27 ~ 1f.hollow cubes of the 3f.r.cube
32 ~ 3f..r.tet.,w.s.
36 ~ total r.lines, 3f.r.sph.,w.s. + 3f.tet.,w.s., s.s.s.,c.sectors + t.s.c.,c.sectors
48 ~ 3f.r.sph.,sh.,r.s., 3f.r.tet.,sh.,r.s., l.c.7,r.s., s.s.s.,r.a., t.s.c.,r.a., 4f.3d.tri.,i.s., 4f.3d.tri.,i.s.i.
54 ~ nfc.,l.c.7. + n.f.c.,s.s.s.,r.s. + n.f.c.,t.s.c.,r.s., f.c.,l.c.7 + f.c.,s.s.s.,r.s. + f.c.,t.s.c.,r.s.
64 ~ 1f. hollow cubes of the 4f.c.cube
72 ~ 4f.3d.r.tri.,sh.o., 4f.3d.r.tri.,sh.i., n.f.c.,l.c.7 + n.f.c.,s.s.s.,r.a. + n.f.c.,t.s.c.,r.a., f.c.,l.c.7 + f.c,s.s.s.,r.a. + fc.,t.s.c.,r.a.
81 ~
96 ~ 4f.3d.r.tri.,i.s. + 4f.3d.r.tri.,i.s.i.
108 ~ 3f.r.cube,sh., 3f.r.cube,i.s., 3f.r.cube,i.s.i., 3f.r.sph.i.s., 3f.r.sph.,i.s.i., l.c.7 + s.s.s.,r.s. + t.s.c.,r.s.
128 ~
144 ~ l.c.7 + s.s.s.,r.a. + t.s.c.,r.a., 4f.3d.r.tri.,sh.o. + 4f.3d.r.tri.,sh.i.
162 ~ 3f.r.cube,sh.o. + 3f.r.cube,i.s., 3f.r.cube,sh.i. + 3f.r.cube,i.s.i.
192 ~ 4f.c.cube,sh., l.c,7, + s.s.s.,r.a. + 3f.sph.sh.,r.s. + 3f.r.tet.sh.,r.s.
216 ~ 3f.r.cube,i.s. + 3f.cube,i.s.i., 3f.r.sph.,i.s. + 3f.r.sph.,i.s.i.
243 ~
256 ~
288 ~ 4f.3d.r.tri.+ t.s.c.,r.a., 3f.r.sph.,i.s.,i.s.i. + 3f.r.tet.i.s.,i.s.i.
324: 3f.r.cube
384 ~ 4f.3d.tri. + t.s.c.r.a. + l.c.7. + s.s.s.,r.a.
432 ~ 3f.r.cube,i.s.,i.si. + 3f.r.sph.,i.s.,i.s.i.
512 ~
576 ~ 4f.c.cube,.i.s.,i.s.i.
768 ~ 4f.c.cube, w.s.v.e., (total r.a. of rainbow equation)-3f.r.cube


