Rainbow Equation 3D Plane Time Axis
b.=3d, plane axis=(3rd eye open)+(time symmetry co-incident)| Moving along the axis of time/no-time the observer connects the polarities of the plane diagram Time Symmetry Coincidence – to learn “flow and experience over time”, with the 3D models 3F 3D Rainbow Triangle – “conscious/sub-conscious mind” and White Symmetry Vector Equilibrium – “universal mind.” |
The Rainbow Equation is an equation of balance, symmetry and harmony. Each part of it flows with the rainbow spectrum of color and operates synergistically from central perspectives. The 3F Rainbow In the Rainbow Equation the axis that has been referred to as the “Time/No-Time Axis” is a complementary between the second the third dimensions of expression. In essence they are a singular expression of the same process as thought moves from space's center, that is zero dimension, through lines of intention (1D), forming in planes of manifestation (2D) and forming the observer's reality completely manifesting in the third dimension. The fourth dimension is also represented along the time/no-time axis. Here in the Third Eye Open process the observer sees a blending back into the space from which no time came and the time reality of manifestation to which it is going. Moving along the axis of time/no-time the observer connects the polarities of the plane diagram Time Symmetry Coincidence – to learn “flow and experience over time”, with the 3D models 3F 3D Rainbow Triangle – “conscious/sub-conscious mind” and White Symmetry Vector Equilibrium – “universal mind.” These polarities flow from the experiential field of time to the universal mind. The symmetry of the time/no-time axis is realized in the equational blending of each pole – plane/3D.
On the plane side of the (b.) plane/3D axis is the Time Symmetry Co-incidence (t.s.c.). The t.s.c. blends several rainbow aspects together in its counting to form rainbow equations. On the plane side facing outwardly the t.s.c. combines tri-secondary combinations (tri.s.c.), curved lines (c.l.), straight lines (s.l.) and quad-secondary combinations (quad. s.c) and rainbow sectors (rainbow sectors).
On the opposite side facing the 3F Rainbow Cube, the
same equational standards are presented substituting
primary combinations (p.c.) to show complement
polarities on both sides of the t.s.c. In the same
manner of the other plane diagrams, the t.s.c. also
equals 4 neutral polarity rainbows per color and
rainbow aspect. Thusly, the Rainbow Equation for Time Symmetry Co-incidence is as follows:
n.f.c., total=(tri.s.c.,c.l.=6)+(tri.s.c.,s.l.=6)+(quad.s.c.,r.s.=12)...+
f.c., total=(quad.p.c.,c.l.=6)+(quad.p.c.,s.l.=6)+(tri.p.c.,r.s.=12)
=(4n.=48)
| The 4F 3D Rainbow Triangle is a reflection of the process of time/no-time within the sub-conscious and conscious mind. |
On the other pole of the time/no-time axis is 3D. The process continues to manifest with the experiential field from the conscious and universal mind. The 4F 3D Rainbow Triangle (4f. r.t.) is a reflection of the process of time/no-time within the sub-conscious and conscious mind. The 4f.r.t. combines together tri. and quad. color combinations along its three 3D sides to form a blending of secondary and neutral rainbow polarities. There are 8 half cubes along each of its three sides adding up to a total of 24 half cubes or 12 full cubes when combined. Once again the number 24 figures prominently into the overall mathematics of the Rainbow Equation. The hollows, that is in-between sectors facing in (i.s.i.), are primary polarity rainbow colors, while the shell colors are secondary polarity colors. In the 4f. r.t. the tri.-neutral colors equal the number of tri-primary colors and the quad.-neutral colors equal the quad.-secondary colors. Equationally, this is expressed: tri.n.=tri.p., quad.n.=quad s. The combination of tri-primary and quad-secondary add up to 1 neutral polarity rainbow: tri.p+quad s.=1n. This balance of colors is in correspondence to the interconnectedness of 3 and 4 colors of the rainbow. Therefore, 2 primary plus 2 secondary equal 3 neutral rainbows: (2p.+2s.=3n.), in correspondence to the 4,3 painted rainbow structure.
In the 4f.
r.t. The shell sectors, in the second combination
colors, add up to 8 primary polarity rainbows
(8*9=72). This is added to the shell inside colors (sh.i.)
of 8 primary polarity rainbows (8*9=72). The combination of the shell inside and outside colors is 12 neutral rainbows – a total of 144 sectors. The rainbow equation for this is: (sh.o.=s.c.,8p.) + (sh.i.=p.c.,8s.) =12n=144.
| The number 24 figures prominently into the overall mathematics of the Rainbow Equation. |
Looking at just the inside sectors (i.s.) and the in-between sectors facing in (i.s.i.) that are not part of the shell, the observer counts 8 quad.-secondary rainbows. This includes only the “quad-colors” of 8 neutral polarity rainbows: (8*4=32 quad.-sectors). Quad. colors are red-yellow-blue-indigo. These quad.-colors are added to the i.s.i. “tri.-colors” for a total of 8 neutral tri-rainbows with the colors of orange-green-indigo. (8*3=24 tri.-sectors).
Combining both the quad. and tri. colors the rainbow equation reads:
(i.s.=8quad.s.=8quad n.) + (i.s.i.=8tri.p.=8tri.n) =8n=96.
Therefore, the combination of all the sectors of the 4th Frequency 3 Dimensional Rainbow Triangle equals 240 sectors or 20 neutral rainbows: (12n+8n)=20n or (144+96)=240.
The other 3D model of the plane/3D axis fits symmetrically into the 4f.r.t. It is the White Symmetry Vector Equilibrium (w.s.v.e.). The w.s.v.e. is composed entirely of white sectors inside and out. The w.s.v.e. is a model of symmetry planes composed of squares and triangles upon its surface. A symmetry plane is a plane that can be “folded” over and produce an exact reflection of itself. When one folds a square connecting its opposing corners the symmetry of two equally sized triangles are produced. Folding along the opposing corners forms an “X” in the folded area and four triangles. The other symmetry of a square is folding and then unfolding it equally top to bottom and left to right producing a “+” and four equally sized squares. Using this logic of symmetry each square plane of the w.s.v.e. produces a total of 8 symmetry planes per side.
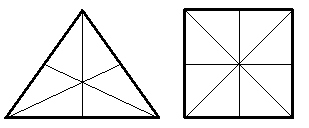
A triangle produces six symmetry planes when folded equally into the center from its points and the midpoints of its outer lines. This produces six equally sized “pie” sections for a total of 6 symmetry planes for one side and 12 for both sides of a whole triangle.
All of the triangles and squares are
“symmetry-sectored” in this manner producing either
six or eight smaller sectors per unit per plane
side. Upon the outside of the shell (sh.o) of the
w.s.v.e. are 6 squares and 8 triangle white sectors
for a total of 14 sectors. As with all planes of the
Rainbow Equation both sides are counted, meaning the
shell inside (sh.i.) complement the shell outside.
Each of these 14 sectors are symmetry-sectored into
6 or 8 smaller sectors per side. 
On the outside
of the w.s.v.e. 4 hexagons are outlined that form an
internal matrix of 4 hexagonal planes. These
equilateral hexagons are defined by the 12 apex
points of the w.s.v.e. Folding along the six points
of each hexagon following the symmetry-sectored
process produces 12 “pie” sectors per side or 24
counting both sides (4 equilateral hexagons*24)=96.In the Rainbow Equation the w.s.v.e. shell, in-between and in-between-ins sectors are thusly expressed:
(sh.o.=96=8n.)+(sh.i.=96=8n.)=16n....+...(i.s.=288=24n.)+(i.s.i.=288=24n.)=48n....=64n.=768
also expressed as:
(sh=192ws)+(i.s.=288ws)+(i.s.i=288ws)=768w.s.=total w.s.v.e.
w.s.v.e. subsets show the process through which the total arrives:
w.s.v.e. shell =
sh.o.=6 squares, symmetry-sectored into 8 sectors each, =(6*8)=48w.s....+...
sh.o.=8 triangles, symmetry-sectored into 6 sectors each,=(6*8)=48w.s....+...
sh.i.=6 squares, symmetry-sectored into 8 sectors each, =(6*8)=48w.s....+...
sh.i.=8 triangles, symmetry-sectored into 6 sectors each,=(6*8)=48w.s.
=192w.s.=total shell.
w.s.v.e. in-between sectors=
8 hexagons, symmetry-sectored into 12 sectors each,= (8*12)=96w.s....+...
12 non-equilateral hexagons, symmetry-sectored into 12 sectors each, =(12*12)=144w.s...+...
6 squares, symmetry-sectored into 8 sectors each,=(6*8)=48w.s....+...
=288w.s.=total in-between sectors.
w.s.v.e. in-between-in sectors=
8 hexagons, symmetry-sectored into 12 sectors each,=(8*12)=96w.s....+...
12 non-equilateral hexagons, symmetry-sectored into 12 sectors each, =(12*12)=144w.s...+...
6 squares, symmetry-sectored into 8 sectors each,=(6*8)=48w.s
=288w.s=in-between-in sectors
